Oligopolies and Tacit Collusion
Oligopoly
- We’ve discussed how firms can raise profits above the competitive level by colluding
- Collusion amongst firms can be tacit or explicit
- The easiest way to model collusion is with oligopoly, which occurs when a small number of firms produce a homogeneous product
- For simplicity, we’ll assume that an oligopoly only consists of two firms (i.e. duopoly)
- Oligopolies must have mutual interdependence
- All firms must be aware of each other’s prices, and care about their actions
Nash Equilibrium
- In order to better understand mutual interdependence, we need some game theory
- Nash equilibrium occurs when no player has incentive to unilaterally deviate from their current strategy
- A Nash equilibrium consists of a strategy for every player
- Suppose we want to determine if a set of strategies constitutes a Nash equilibrium
- We want to see if any player has incentive to unilaterally deviate from their current strategy (i.e. can one player increase profit by unilaterally changing their strategy)
- We’ll do this for every player in the game
- If no player can better their profit unilaterally, then we have found a Nash equilibrium
Example
- Consider the following game between player 1 and player 2
- Each player can select either a high price (H) or a low price (L)
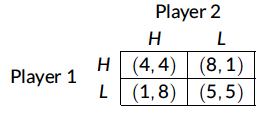
- The Nash equilibrium occurs when both player 1 and player 2 price high, resulting in a payoff of 4 to each player
- Neither player can unilaterally deviate and increase their profit
Example Question
Would it be easy or difficult to maintain effective collusion if two dupolists faced the following profit matrix?
| Firm B’s Action | |||
|---|---|---|---|
| High Price | Low Price | ||
| Firm A’s Action | High Price | 1000, 150 | 700,100 |
| Low Price | 800, 50 | 500,75 |
Does there appear to be a dominant firm in this industry? Does Firm A have a dominant solution to this game? Does Firm B have a dominant solution to this game?